Understanding Derivative Pricing: A Key Element of Financial Risk Management
In today’s dynamic financial markets, derivatives are essential tools in risk management, offering tailored solutions for hedging, speculation, and arbitrage. But how exactly is the price of a derivative determined? At Amsshare, we aim to demystify this process using industry-standard pricing methodologies, while leveraging our expertise in custom risk solutions and AI-driven financial modelling.
What Are Derivatives?
A derivative is a financial instrument whose value is contingent upon an underlying asset, such as equities, bonds, interest rates, or currency exchange rates. Common types include futures, forwards, options, and swaps. These instruments play a crucial role in managing exposure to market risk, credit risk, and liquidity risk, and are widely used in investment funds and institutional portfolios.
The Role of Derivatives in Risk Management
Derivatives can be structured to serve a variety of financial objectives:
-
Hedging: Protect against adverse price movements in the market.
-
Speculation: Capitalise on market forecasts to generate profits.
-
Arbitrage: Exploit price discrepancies across markets.
-
Financial Engineering: Customise payoff structures to suit investor needs.
These applications underscore the importance of derivatives in financial risk management strategies.
Pricing Derivatives: The No-Arbitrage Principle
A fundamental concept in derivative pricing is the principle of no arbitrage. This principle asserts that in an efficient market, it should not be possible to earn risk-free profits. Prices must be aligned across markets to prevent discrepancies. When applied to derivative instruments, this principle ensures fair value estimation through replicable strategies.
Two Core Pricing Methods
Amsshare supports derivative valuation using two principal methods: the replicating portfolio approach and risk-neutral valuation. Both are grounded in the no-arbitrage framework, which aligns with regulatory and market efficiency standards.
1. The Replicating Portfolio Method
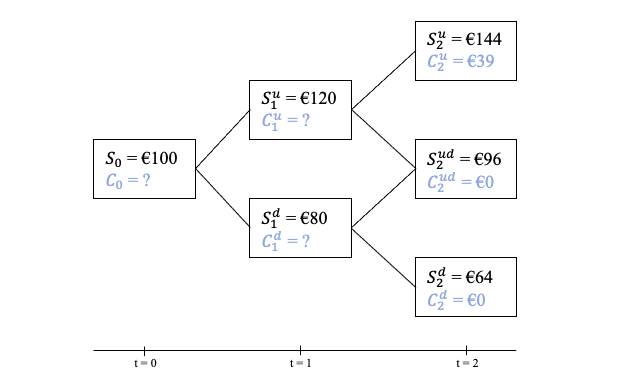
This method involves constructing a portfolio using the underlying asset and a risk-free investment (e.g., treasury bills) that mirrors the payoff of the derivative. The key is to determine the right mix—known as delta and B—that replicates the derivative’s outcome under all market scenarios (up or down states).
A step-by-step approach involves calculating delta (exposure to the underlying asset) and B (capital allocation to the risk-free asset). By using a binomial tree model, as illustrated in Amsshare’s educational materials, one can determine the derivative’s value at each node until reaching the present value.
2. The Risk-Neutral Valuation Method
Risk-neutral pricing simplifies the above approach by using artificial probabilities that assume investors are indifferent to risk. Here, the expected value of the derivative’s future payoff is calculated using risk-neutral probabilities and then discounted at the risk-free rate.
This method is especially effective for complex or large-scale pricing models due to its computational efficiency. It enables practitioners to calculate the present value directly from the maturity payoffs, making it an ideal tool for AI solutions and algorithmic pricing models used in modern finance.
Practical Advantages and Applications
While both pricing methods lead to the same theoretical outcome, risk-neutral valuation offers practical advantages in speed and scalability. It enables automated systems—such as Amsshare’s in-house AI risk assessment tools—to price options and other derivatives across vast datasets quickly and accurately.
Furthermore, this pricing framework supports robust decision-making for asset managers, treasurers, and compliance teams, helping them meet the demands of effective risk solutions and regulatory compliance, such as for a UCITS fund or a tailored KID-compliant product.
How Amsshare Can Help
With extensive expertise in financial risk management, AI-driven pricing models, and custom risk solutions, Amsshare empowers clients to navigate the complexities of derivative instruments. Our team supports projects ranging from option valuation models to portfolio risk simulations and regulatory reporting.
By integrating cutting-edge techniques with practical applications, we help financial institutions, investment funds, and corporate treasuries manage their risk exposures more effectively and strategically.