A brief summary
An introduction to IFRS-9
In today’s rapidly evolving financial landscape, effective risk management is more crucial than ever. With the implementation of the International Financial Reporting Standard 9 (IFRS 9), financial firms such as banks are required to move from a static, historical view of default risk—Through-the-Cycle (TtC) Probability of Default (PD)—to a dynamic, forward-looking Point-in-Time (PiT) PD approach. This transition represents not just a regulatory shift but a critical step toward more resilient, data-driven lending practices. There is an interesting overlap between this analysis of historical data and the services we provide for Key Information Documents (Essentieel Informatie Document) of financial firms, where scenario calculations must be based on historical NAV data.
However, the IFRS 9 framework leaves a key challenge unanswered: how should banks select the right forecasted macroeconomic variables (MEVs) to adjust their TtC PDs to PiT PDs? Enter the LASSO BIC method—an innovative machine learning technique that automates and optimises this variable selection process, improving both efficiency and accuracy. This article is a publication of my MSc thesis (Thomas van den Berg,) in which I describe the application of the LASSO BIC method to European corporate loan data, offering a compelling new strategy for financial institutions looking to refine their Expected Credit Loss (ECL) calculations. The computation of the Expected Credit Loss (ECL) is a core component of credit risk modelling and directly determines the level of required provisions for financial firms.
IFRS 9 replaces the outdated IAS 39 standard by introducing a more forward-looking approach to credit risk. At its core, IFRS 9 requires banks to estimate expected credit losses (ECL) using a blend of past performance, current conditions, and future macroeconomic forecasts. One of the essential components in this model is the Probability of Default (PD). Yet, the regulatory framework offers no guidance on how to select these MEVs. Most banks rely on expert judgment or manual regression analysis—methods that are labor-intensive and prone to bias or inefficiency.
The quantitative techniques used in this research also reflect the type of expertise we apply in our AI agent modelling services, where we develop AI tools to support data-driven decision-making in finance.
The proposed approach: the LASSO BIC method
In this research, I propose the Least Absolute Shrinkage and Selection Operator with Bayesian Information Criterion (LASSO BIC) as a solution. This machine learning method automates the selection of macroeconomic variables that best explain variations in corporate loan default rates.
Key advantages of the LASSO BIC model:
-
Automation: No need to manually test endless variable combinations.
-
Efficiency: Handles large datasets and high-dimensional data with ease.
-
Parsimony: Avoids overfitting by penalizing model complexity.
-
Interpretability: Selects only the most predictive variables.
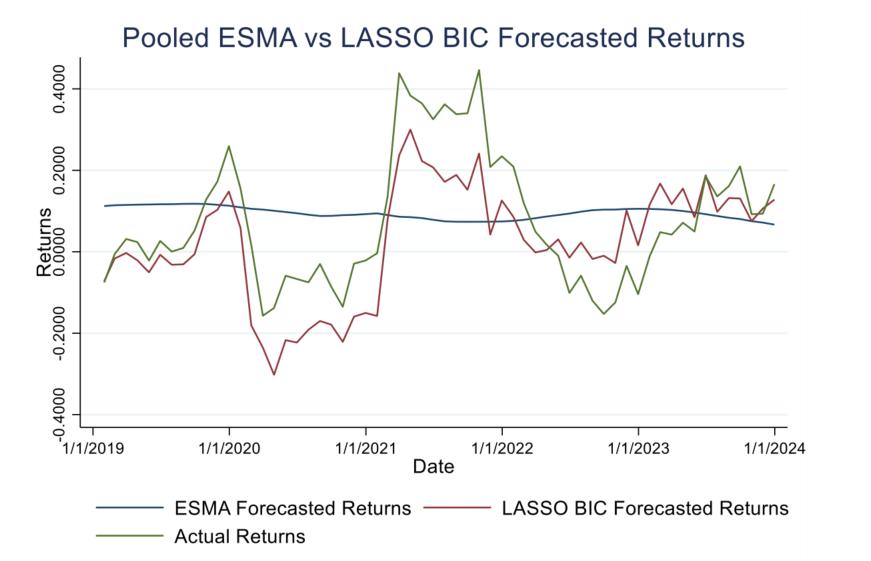
By applying LASSO BIC to European aggregated corporate default rate data from Moody’s (2005–2023), I identify key macroeconomic indicators that are consistently influential in default forecasting—most notably the 3-month Euribor rate (lagged by 10 months) and the corporate bond spread (lagged by 8 months).
Data sources
-
Default Rate Data: Monthly European corporate loan default rates (Moody’s, 2005–2023)
-
Macroeconomic Variables: Seven MEVs from ECB, Eurostat, and FRED:
-
3M Euribor (interest rate)
-
Industrial Production (proxy for GDP)
-
Inflation (HICP)
-
Trade Volume (XVOL)
-
Unemployment Rate
-
Government Bond Spread
-
Corporate Bond Spread
-
Data prepration
-
Stationarity Tests: All variables were differenced to ensure stationarity using the Augmented Dickey-Fuller test.
-
Lag Inclusion: Up to 12 lags per MEV were included to capture delayed effects on default rates.
Selection method
LASSO BIC identifies which macroeconomic indicators have the most explanatory power for each year. The model is recalibrated yearly using an expanding estimation window—adding new data to improve the robustness of predictions over time.
Model validation
Each selected model is tested against OLS assumptions:
-
Multicollinearity (VIF test): All models passed.
-
Autocorrelation (Portmanteau test): Managed via HAC standard errors where necessary.
-
Heteroskedasticity (Breusch-Pagan test): Addressed with robust errors.
-
Normality of Residuals (Shapiro-Wilk test): Violations mitigated using the Central Limit Theorem.
Key findings
Top predictive MEVs:
-
10th lag of 3M Euribor rate – consistently significant in all models
-
8th lag of corporate bond spread – highly predictive in 4 out of 5 years
-
5th lag of industrial production – negative correlation with defaults
-
11th lag of inflation (HICP) – positively correlated with default risk
These results confirm hypotheses from both financial theory and prior empirical studies. For example, higher interest rates and inflation tend to increase credit risk, while economic growth (as measured by industrial production) reduces it.
Prediction accuracy tests
I evaluate the LASSO BIC model’s forecasting power using:
-
Unbiasedness Tests: Ensures no systematic over/under-estimation
-
Mean Squared Prediction Error (MSPE): Measures predictive accuracy
-
Efficiency Tests: Confirms forecasts can’t be improved using available information
Overall, the LASSO BIC models provide accurate and efficient forecasts, though extreme events like financial crises still pose a challenge-an inherent limitation in all predictive modelling. This thesis delivers a practical and scalable solution for financial institutions seeking to improve compliance with IFRS 9 while reducing model risk and operational costs.
Key takeaways for financial firms:
-
Efficiency: Automate macroeconomic variable selection using LASSO BIC.
-
Relevance: Reassess selected MEVs regularly as their predictive power may change.
-
Scalability: Apply LASSO BIC across different portfolios and geographies.
-
Integration: Pair LASSO BIC with internal or external macro forecasts (e.g., ARIMA, EBA projections) to compute PiT PD adjustments.
Conclusion
By introducing the LASSO BIC method for macroeconomic variable selection in the context of IFRS 9, this thesis marks an advancement in risk modelling. For financial professionals, regulators, and data scientists, this work offers both theoretical depth and practical value. It demonstrates how combining rigorous methodology with innovative tools can lead to more responsive, accurate, and efficient models of credit risk. As the financial industry continues to adapt to economic shocks, regulatory demands, and technological transformation, smart tools like LASSO BIC will play an increasingly vital role in safeguarding financial stability.